- Srp 1, 2014
- Pavel Felgr
- Velká pyramida
- 0 Comments
Různí spisovatelé již dříve zmínili poměr 7:11 pro exteriéry pyramid (i Velké pyramidy). Tento poměr je dokonce i v Petrieho knize Pyramids and Temples of Gizeh (Pyramidy a chrámy v Gíze). A poměr 7:11 pro kameny vnějšího pláště Velké pyramidy se objevil, protože pyramida je postavena za použití matematické konstanty pí jako modelu nebo ukazatele.
Nejjednodušší poměr pí, který poskytuje hodnoty celých čísel na obou stranách této matematické konstanty je 7:22. Odtud byl převzat poměr 7:11 pro vnější rozměry pyramidy. Zvýšení hodnoty z 11 na 22 je kvůli vzorci pro kruh, který byl vynásoben 2 (tedy: 2 x Π x r).
Kompletní řešení záhady malých šachet říká, že čísla pro úhly šachet také reprezentují stejné poměry pí. Samotné šachty se odchylují nahoru či dolů o několik desetin stupně, ale průměrná trajektorie je celkem spolehlivá. Pokud předpokládáme, že architekt stavěl šachty v úhlech s přesností na 0,5°, pak jsou úhly čtyř malých šachet, které se rozvětvují z hlavní komory Velké pyramidy, tyto: 45°, 39,5°, 39,5° a 32,5°.
Velká pyramida a sklony šachet v ní
A pokud zakreslíme tyto úhly a délky do té části pyramidy, kde se šachty kříží, stane se něco zajímavého. Stoupání každé šachty je přesně 70 královských loktů (1 egyptský královský loket = 52 cm). A 70 královských loktů je přesně 1/4 výšky samotné pyramidy dlouhé 280 královských loktů. Lineární rozměry malých šachet, včetně důležitého svislého stoupání v loktech, souvisí matematicky i s rozměry v loktech samotné pyramidy.
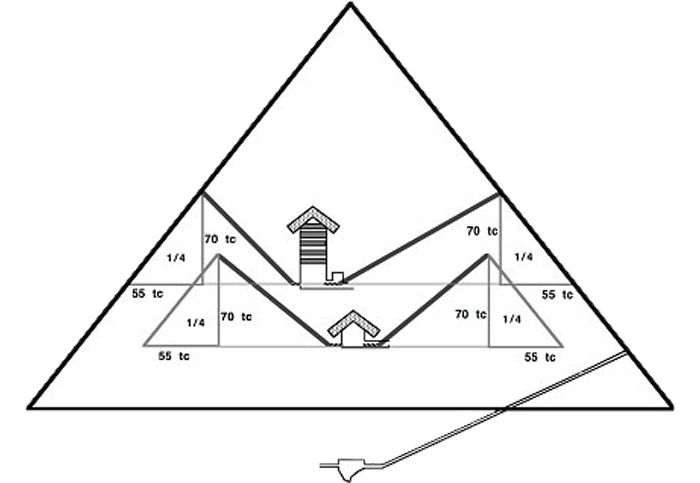
Svislé stoupání všech malých šachet je 70 královských loktů,
tj. 1/4 z výšky Velké pyramidy dlouhé 280 královských loktů
Pozoruhodná symetričnost šachet Velké pyramidy
A zatímco tohle všechno je docela důmyslné, v symetričnosti šachet je toho ještě mnohem více. Pokud odečteme větší úhel od toho menšího na každé straně pyramidy (na severní a jižní straně), číselné rozdíly mezi úhly jsou následující:
45° mínus 39,5° = 5,5°
39,5° mínus 32,5° = 7°
hodnota 5,5 je 1/4 z 22.
Překvapivě je zde opět stejný poměr pí čísel (7:11 nebo 7:22), ale v tomto případě se jedná o úhel, nikoliv o délku. Znovu můžeme vidět celou povahu úhlu těchto šachet. Nejen že jsou lineární rozměry šachet úzce spjaty s rozměry pyramidy, rozměry pyramid jsou také úzce spjaty s číselnými rozdíly úhlů. Toho je až překvapivě obtížné dosáhnout, zvlášť pokud je výchozím bodem pro všechna tato čísla matematická konstanta pí! Částečně toho lze dosáhnout tak, že ústřední úhel 39,5° může být odvozen z (2 x Pi)2 a také z arcsin z 7/11 (nebo 1/2 pí).
Vyvrácení teorie, že šachty míří na hvězdy
A ten opravdu důležitý výstup ze vší této matematické symetrie je ten, že to úplně vyvrací teorii šachet mířících na hvězdy. Čtenáři mohou jasně vidět, že délky a úhly malých šachet ve Velké pyramidě používají matematickou konstantu pí jako základní kritérium pro plán stavby. Jsou to šachty založené na pí. To ale znamená, že úhel jejich stoupání je stanoven prostřednictvím pí a ne polohou konkrétních hvězd v určitém období.
Úhel sklonu šachty podle pí nemůže mířit ke konkrétní hvězdě, může pouze mířit v pevně daném úhlu a jakékoliv směřování ke hvězdě je tedy jen náhodné. Pokud však můžete libovolně změnit období, se kterým se mění i úhel stoupání hvězdy prostřednictvím precese, pak můžete teorii šachet mířících na hvězdy učinit platnou. Pokud objevíme šachtu s úhlem 55°, bude odpovídat pozici Orionu okolo roku 4 450 př.n.l. A tak můžeme pokračovat donekonečna – pro jakýkoliv úhel a jakékoliv období. Teorie šachet mířících na hvězdy je nekonečně flexibilní a proto také nekonečně nepravdivá.
Zdroj: Ancient Origins; Autor: Ralph Ellis; Český překlad: Alííí

